Soit \(X\) une v.a. À valeur dans \({\Bbb N}\).
Déterminer toutes les lois possibles de \(X\) telles que $$\forall n,m\in{\Bbb N},\quad {\Bbb P}(X\geqslant n+m\mid X\geqslant n)={\Bbb P}(X\geqslant m)\gt 0.$$

Pour \(n=m\), la relation se transforme en une relation de puissance.

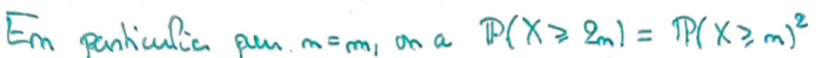
Par récurrence, on montre que la probabilité d'être supérieur à un nombre s'écrit comme une puissance de la probabilité d'être supérieur à \(1\).

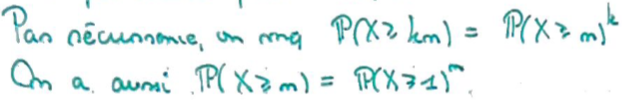
On peut maintenant montrer par récurrence que cette loi s'écrit comme une loi géométrique.

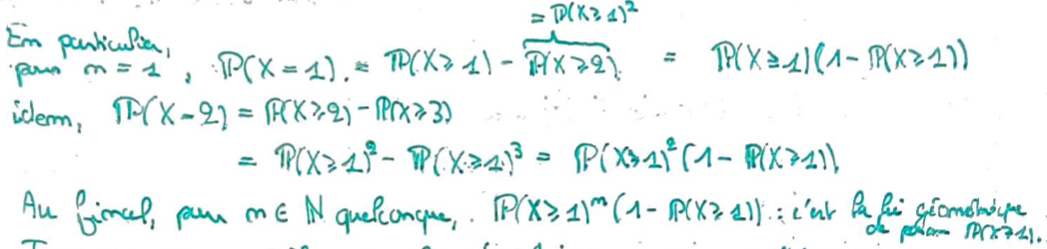
Réciproquement, les lois géométriques sont sans vieillissement, donc elles correspondent exactement.